![]()
FORCES IN SWIMMING -- A RE-EVALUATION OF CURRENT STATUS: PART III
PART III
PROPULSIVE FORCES
Bernoulli's Principle
Bernoulli's Principle states that fluid pressure is reduced whenever the speed of flow is increased. The difference in pressure between two flows is described as dynamic lift. The most common application of Bernoulli's Principle is to the shape of an asymmetrical airplane wing. A curved upper surface produces a faster flow of air than does a lower flat or concave surface, resulting in a pressure differential. Lift of this nature acts on the body in a direction perpendicular to the path of the object movement through a fluid.
Typical references to the appropriateness of this principle to swimming have appeared in the literature. Maglischo (1982) accounted for lift as follows:
"The amount of lift force is proportional to the difference in pressure between the two wing surfaces which is, in turn, dependent upon the shape of the wing surfaces and the forward speed of the airplane." (p. 12)
Counsilman (1971) stated:
"A wing provides aerodynamic lift through the camber (curvature) of its surfaces. Because the upper surface is more highly cambered than the lower surface, the air moving over the top surface is forced to move more quickly. This results in a lower pressure on the upper surface as compared with the lower surface and results in aerodynamic lift (Bernoulli's Principle)". (p. 61)
These references are typical of the allegiance of most swimming "authorities" to the lift force derived from the principle. Such references are misleading (Sprigings & Koehler, 1990, p. 237).
The method of difference is often used as a logical procedure to justify the appropriateness of Bernoullian lift in swimming. What authors typically attempt do is explain why drag cannot possibly be a "good" force for swimming. This is done by analogizing devices that are not particularly successful in propelling efficiency and showing their similarities to the actions of swimmers. By eliminating them as propulsive models and the drag component that was inefficient in each circumstance, it is deduced that Bernoullian lift must be the remaining force that is useful. There are three common analogies that continue to be reproduced in the literature (e.g., Schleihauf, 1975a).
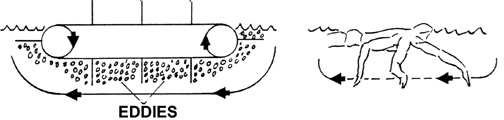
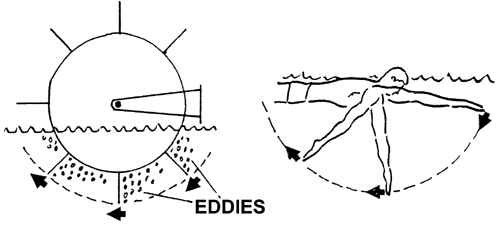
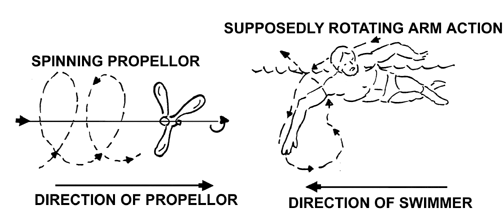
These three examples are invalid and therefore, do not serve to eliminate the possibility that drag forces can be beneficial in swimming strokes.
It should be realized that the original promotion of Bernoulli's Principle as the "reason" why swimmers move forward was conjecture. What is needed is verification that the propulsive forces of swimming are predominantly lift and that the hand and forearm from the radial and ulnar edges are lifting surfaces if the Bernoullian interpretation is to be supported.
If Bernoulli's Principle was the appropriate model for explaining propulsion in swimming, the following would have to be true:
The postulation of Bernoulli's Principle for creating dynamic lift is inappropriate for hypothesizing about swimming propulsion. Evidence now is available to refute the original hypothesis of its appropriateness. It is a tragedy that it has remained popular for so long for it has lead those who "reason" rather than test techniques down an incorrect path of inquiry and postulation. A better theoretical basis for propulsion needs to be formulated. Bernoulli's Principle cannot account for what happens in swimming propulsion. Sprigings and Koehler (1990) reacted to the lift-force-only postulation as follows: " . . . to dwell exclusively on the lift component without any attention to the drag component would be an analytical blunder" (p. 238).
Lift and Drag Forces
It is generally recognized that drag and lift forces have to be considered as contributing to the propulsion of swimmers. To emphasize lift and minimize drag as quoted above is nonsensical. Swimmers should maximize forces that produce propulsion. Sprigings and Koehler (1990, p. 242) proposed an explanation employing Newton's Second and Third Laws to account for drag and lift forces in swimming. As a swimmer pushes backward the fluid under the hand is slowed by the angle of the hand (angle of attack) and frictional forces. When the angle is acute, the slowing is small producing small lift and drag forces. When the angle is larger, the slowing increases, as does the reaction force. The reaction force can be broken down into lift and drag components. The slowing of the fluid in this manner is also embellished by frictional drag from the surface of the hand and forearm as well as form drag caused by the size of the hand and forearm as it moves through the water. Wood (1977) explained this phenomenon as follows:
"When a body moves through a fluid the force acting on it does so directly backwards and is called drag or form drag. As the oncoming fluid strikes the body it is deflected outwards and attempts to follow the body contour. In the case of a streamlined body it is able to do this relatively easily. In the case of a non-streamlined shape, for example, an oar or a paddle or a hand held so that as much cross sectional area as possible is positioned perpendicular to the line of flow, the fluid is unable to achieve the sharp turn at the edge of the body and flow separation takes place giving rise to whirling and eddying pockets, or a wake behind the body extending in the direction of the flow.
An interesting feature of these pockets is the low pressure that is obtained in these volumes. This low pressure coupled with the build up of pressure as the fluid strikes the front of the body leads to a resultant pressure in the original direction of the fluid flow. This resistance is called form drag." (p. 5)
The Newtonian interpretation of propulsion through water is based on the impulse-momentum relationship (Newton's Second Law). Basically, any change in the magnitude or direction of the water's momentum as a result of its disturbance by a swimmer's body segment(s), is a direct result of an impulse (i.e., force applied for a period of time) applied to it. Newton's Third Law dictates that there must be an equal but opposite impulse back on the swimmer's segment(s) that is then broken down into two perpendicular components, lift and drag. Drag is the force component parallel to and in the same direction as the relative fluid flow prior to segment contact. Lift is defined as the component of force perpendicular to the drag component. To use the Newtonian approach to understanding propulsion, one only has to visualize the resulting changes in magnitude and direction of the disturbed water's momentum as it moves (relatively speaking) past the swimmer's segments, and then apply Newton's Third Law. On the other hand, Bernoulli's Principle is based on the work-energy theorem that imposes serious limitations on its ability to predict lift in a practical situation such as the swimming stroke. It should be recognized that Bernoulli's Principle is not capable of predicting drag forces.
In still water drag acts in the opposite direction to the line of motion of the foil (i.e., hand-forearm) and it resists the motion of the foil. Figure 4 illustrates the various components to be considered with the forces that occur on the hand and/or forearm in all competitive swimming strokes.
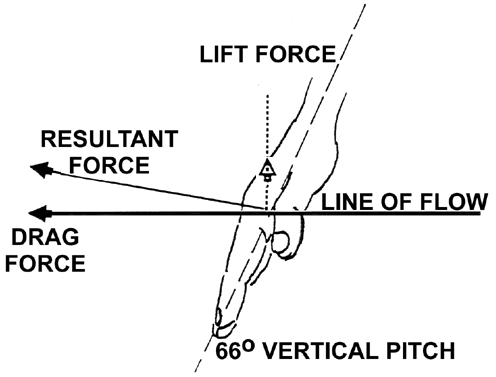
Using the Newtonian model, drag is composed of three parts: induced drag, frictional drag, and form drag. Each is related to the angle of attack and when combined form the "coefficient of drag". This model can be used to predict both drag and lift components of force in the action of a hydrofoil (i.e., a swimmer's hand and forearm).
The major consideration in this interpretation is the direction in which the hand is moving. That direction is the flow line. Drag forces react directly opposite to the flow line and lift forces react at right angles. Figure 5 illustrates some of the force directions generated by positions of the hand in a crawl stroke. The data for the figure were obtained from Wood (1977). It can be seen that how the hand is pitched determines the direction of the forces that are created.
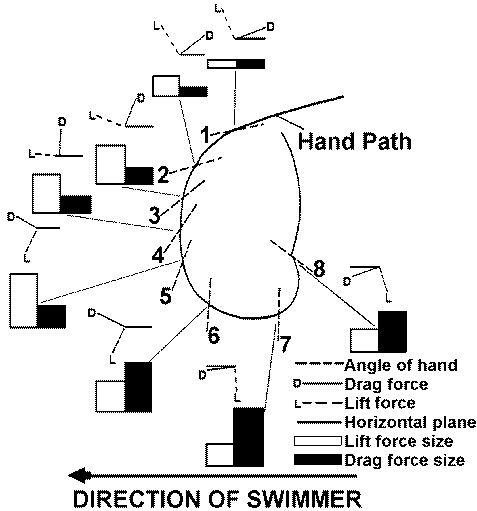
The data in Figure 5 are limited but do represent the features of a crawl stroke action. The major limitations are:
Despite these limitations, several features are notable.

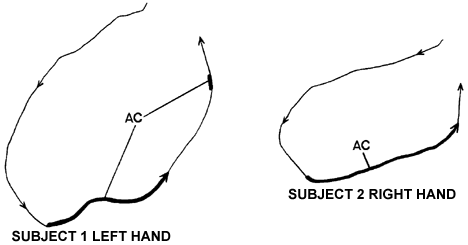
What exist in swimming actions are combinations of lateral and longitudinal forces of both lift and drag. They occur because swimmers do not pull their hands straight back through the water. There is some element of sideways movements in most patterns. In breaststroke sideways movements are accentuated. However, since Counsilman (1970) published pictures of swimmers under water and used those pictures to support the importance of sideways actions (i.e., Bernoullian lift), stroke patterns have changed and performances have improved remarkably. Figure 7 compares underwater pull patterns in the butterfly stroke of Charlie Hickox (Counsilman, 1970, p. 12), who recorded the best time in the world for 200 m butterfly in 1967, and Pablo Morales (Cappaert, 1993) as he swam to victory in the 1992 Olympic 100 m butterfly event.

What is noteworthy about these patterns is the reduced lateral aspect of Morales' action when compared to that of Hickox. It is not known when Hickox achieves a propulsive force but it is known for Morales. When the arms propel Morales, his pull is notably direct. The S- or hourglass shaped pull as proposed in the 1960s is not evident. There is a constant, slightly outward pull path in Morales' action that is most probably caused by adduction of the upper arm and positioning to use extension of the arm in the latter phase of the pull. That is an important phenomenon because often the arm movements of swimmers are modified to accommodate the limitations of the human anatomy, which is poorly constructed for swimming. Given Morales pattern of pull and hand orientation, no Bernoullian lift could account for the propulsive forces achieved or demonstrated.
Another feature of these two pulling patterns is the asymmetry between the arms. There are actions added to an ideal pattern to offset modifying forces so that there is continual propulsion of the swimmer in a straight line. For example, a strong arm is compromised to balance a weaker arm. Because of that compromise, it will be very difficult to find a perfect pattern of movement in any swimmer. At best, modern champion swimmers usually will have a better approximation of an ideal pull than will lesser performers.
The case has been made that Bernoulli's Principle is inappropriate for a basic understanding of the propulsive forces in swimming. A return to Newtonian Laws is warranted. However, that return requires the consideration of drag and lift forces rather than the 1960s' version of contemplating only drag forces. Evidences of a scientific and observed nature are available to support and extend this restated position.
Measuring Arm Forces
The measurement of forces in swimming is difficult. Interactions occur between the many segments involved in normal actions. When an analysis is performed on an isolated segment, misleading conclusions could be developed. Even though the current status of force measurement is much better than it has been, it still leaves much to be desired. In this paper the measurements discussed are in concert with observational analyses of filmed records of swimmers.
In the early and latter stages of a pulling pattern there are actions which have a high vertical component. To develop propulsion, the hand-forearm has to be taken to a sufficient depth and then changed to a path that has a large horizontal component. After the major propulsive forces have been exploited the arm then needs to be raised upward to exit the water. When high vertical component phases enter and leave the horizontal phase, the paths of change are rounded actions that conserve momentum. It is advocated that the early and latter stages of an underwater action should be named "transitions". Observations and reports from swimmers indicate that these transitional stages do not produce propulsion or "feel" like they are propulsive. The term "pull" should be reserved for the effective propulsive phase of the stroke.
Current computer analyses of forces are limited. They analyze the hand only and treat it as an isolated object, not being affected by the forearm or any other part of the anatomy. The entry transitions of crawl stroke and butterfly can generate a small lift force because the hand-forearm can be pitched to produce:
The resultant force from those two components could have some beneficial propulsive contribution even though a significant portion of it is in a vertical orientation. The work of Wood (1977) and Wood and Holt (1979) showed forces that could contribute to and do not impede propulsion are developed if the entry transition movement is markedly downward.
The path that the hand-forearm takes in the underwater phase of a swimming stroke does not always facilitate propulsion. There are forms of action that actually hinder, rather than help, a swimmer. Any time a movement is fractionally or more in the direction of the intended propulsion, a swimmer's progress is partially checked. For example, when a hand enters and continues to extend forward under water in crawl stroke, surface, form, and wave resistances are increased and forces are created that work to impede forward progression. Those detrimental forces detract from the overall efficiency of the swimming stroke and are counter-productive to forward propulsion.
The current techniques of force measurement and estimation for the hand in the entry transition and the body of a pull are satisfactory estimates of what the hand is doing at those stages. However, in the estimate of the exit transition there is a profound weakness and measurements at that stage of force estimation should be viewed cautiously.
In the entry transitions of crawl and butterfly strokes, lift and drag forces are created distally, that is, the water flows from the fingers up the arm. However, at the exit transition, it is the elbow that leads the hand. That means some water may flow down the arm and exit over the finger tips, the exact opposite of what occurs in the entry transition. It is also likely that considerable turbulence will surround the back of the hand.
Measurements of the exit transition forces of the hand have been provided by Cappaert (1993; Cappaert & Rushall, 1994). The analysis considers the hand to be an independent object not attached to an arm. It is treated as a discrete segment. Thus, it is possible to determine angles and velocities of movement and calculate lift and drag forces. However, that is a spurious procedure for analyzing forces on the hand at the exit transition. Because of the leading forearm, it is not possible for water to flow down the arm over the hand to develop an environment conducive to producing marked lift forces. The hand does not function as an isolated object because of its trailing position. Cappaert's analyses illustrate high lift forces and smaller drag forces for that stage of propulsion in almost all crawl stroke and butterfly swimmers. It should be understood that those measures are theoretical and do not apply in this case because of the confounding influence of at least the forearm. Because of that weakness, it is advocated that measures which are reported for the entry transition and the body of a pulling pattern can be considered, however, measures for the exit transition should be ignored until better forms of force estimation can be developed.
When the pulling action can be made in a largely horizontal direction, the orientation of the hand-forearm favors stronger drag forces the more it approaches right angles to the line of propulsion. A pure right angle may not be the most beneficial position while a pulling pattern has the dual function of creating direct propulsion and counteracting rotational forces in any of several directions. Kieren Perkins' (see Figure 8) and Krisztina Egerszegi's (see Figure 10) hand-forearm positions produce very large drag forces in comparison to lift forces. Their positions approach right angles to the intended direction of propulsion. On the other hand, as the angle of the hand-forearm lessens in relation to the line of flow, the drag forces diminish and lift forces become relatively more important (see Hrvoje Baric in Figure 10).
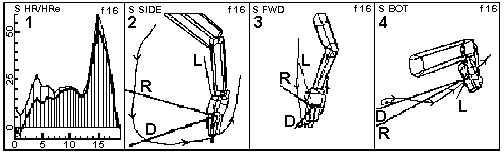
When entry transitions go too deep, the stroking pattern of the body of the pull will likely slip upward either gradually or in steps. Because of the noticeable vertical component rather than a maximized horizontal orientation, drag forces will be reduced and potential power from a better path of movement lost. It is advocated that the tendency to dig deep on the entry should be moderated so that energy expended will be used more efficiently and effectively because of the better alignment with the line of propulsion.
The proportional contribution of lift and drag forces to propulsion in the intended direction of progression is dependent upon a number of factors:
Understanding the forces that contribute to propulsion is not a simple matter. It is not just a case of saying that drag forces or lift forces are only important. It is more a matter of understanding the complexity of the movements in all strokes and then evaluating the position of the anatomy to create the most favorable forms of force to contribute to propulsion in that stage of the pull. However, it would seem that several factors regarding force production need to be considered when evaluating pulling techniques.
Further Considerations
The minimal contribution of lift forces. If lift forces were working fully in the Bernoullian mode, the flow of water across the back of the hand would be undisturbed, that is, the water would be as clear as it is on the palm of the hand. However, anyone who has observed swimmers' pulls underwater can recognize that the "trailing" water on hands is often turbulent and contains bubbles. That means the water behind the hand is being "dragged" in an eddy and is not the clear flowing form necessary for Bernoullian lift. Valiant et al. (1982) explained this observation:
" . . . bubbles and turbulent wake about the hand suggest there is very little opportunity for attached flow, meaning a low potential for creating a lift force component." (p. 397)
When observations of turbulence and bubbles are made, lift forces will not be dominant in contributing to propulsion.
Holt and Holt (1989) tested the hypothesis of flow across the back of the hand generating lift. They attached several fin-like baffles to the back of swimmers' hands. The baffles effectively disrupted the flow across the curved back of the hand and thus, negated lift forces. The effect on crawl stroke swimming speed was minimal (2%). This demonstrated that lift forces were quite minor in their contribution to propulsion.
Figure 8 illustrates Kieren Perkins' left hand pull paths from side, front, and bottom perspectives during the last 100 m of his 1500 m gold medal swim at Barcelona. It can be seen that the path of the finger tips and the position of the hand at the position of maximum pulling force produce more drag than lift force. The drag component is also aligned more in the desired direction of propulsion than is the lift component.
The hand angles in all strokes usually never approach the theoretical best angle for developing lift (37 degrees, Counsilman, 1977, p. 141). The hands of top swimmers in either the vertical or lateral planes do not exhibit that angle during propulsive phases of the pull (see Figure 8 for an example). It should be noted that proposing such an angle is contrary to the required position for Bernoullian lift to occur. Such an advocacy is a further illustration of the confusion that has surrounded lift and drag forces and Bernoulli's Principle.
The hand-forearm propelling surface. Much of the discussion on propulsive forces has concentrated on what the hand does. However, it is very possible that the forearm provides an effective propelling surface as much as does the hand. Coaches have often talked of the "elbows up" position to produce propulsion but often in the context of placing the hand in a better position. However, swimmers are still able to propel themselves forward quite satisfactorily if they swim with a good elbows up position, that is, the forearm is vertical and pushing backward, with fists clenched or hands turned sideways to slip through the water. The role of the forearm in contributing to propulsion needs to be considered more than it has been. If the forearm is effective for contributing to propulsion then those adhering to Bernoullian forces cannot explain its contribution. The forearm is not a lifting surface and it has never been included in any swimming descriptions of lift production.
Cappaert analyzed the lift and drag forces generated by the hands and hands plus forearms in various positional angles and speeds of water flow (Troup, 1992, pp. 93-99). That study was oriented towards focusing on lift forces and in its discussion maintained that orientation. Coefficients of drag and lift as well as absolute forces were measured (see Figure 9). Contrary to the emphasis of Cappaert's discussion, the following factors were demonstrated.

The maximum contributions of drag forces. The side view of pulling patterns of some of the world's best swimmers are presented (see Figure 10) indicating the phase of the strokes where propulsive forces are created (extracted from Cappaert, 1993; Troup, 1991). Propulsion occurs when there are distinct emphases of backward rather than lateral forces. This means that champion swimmers are pushing back against the water rather than emphasizing lateral movements to generate lift. In Troup (1991, p. 113) an example of Summer Sanders' crawl stroke analysis was provided. In both her left and right hand pulls, which exhibited S-shaped patterns, when sideways components were exaggerated her propulsive force decreased. Sideways actions did not facilitate effective propulsion. It should be noted that Summer Sanders' crawl stroke was not reputed to be one of her better strokes.

Coaches are encouraged to conduct their own experiments comparing lift versus drag orientations. They should instruct swimmers to emphasize pushing back against the water so that the hand-forearm combination becomes fixed in the water. It should be pointed out to the swimmers that they are to move their bodies past the fixed position in the water. This should bias the swimmers' strokes towards generating drag forces. Times and number of strokes taken for a distance should be recorded for that orientation. Then swimmers should be instructed to move their hands-forearms through the water in exaggerated S-shaped patterns. That action should facilitate an increase in lift and a reduction in drag. Times and number of strokes taken for a distance also should be recorded for this orientation. The two orientations should be compared for time and number of strokes taken. Swimmers also should be asked which orientation felt best and made them swim fastest. The outcome of this test will be obvious but coaches will also be surprised by the magnitude of the differences.
Pulling patterns. The observed pitches of hands of champion swimmers are more in the range of angles that maximize drag force rather than lift. That contention is supported in data contained in the technical summary of Cappaert's work (Cappaert & Rushall, 1994). It should be noted that hands are rarely, if ever, pitched at 90 degrees. Hand pitch not only has to accommodate propulsion but also has to "correct" for vertical movements involved in hand recoveries and repositioning, breathing, and kicking. All strokes require compromise positions and can never be solely dedicated to propulsion.
What was shown in Cappaert's analysis was an objective verification of the findings of Wood's and Holt's studies. The primary force in the propulsive phase of crawl, back, and butterfly strokes is drag. Any lift force is minor but still important. That one or the other force is totally responsible for propulsion was never found. Wood (1977) offered a reason for this phenomenon:
When the recovery in front crawl is cleared from the water and begins to swing up, out, and forwards, the body is subjected to a rotational effect. This in part is canceled out by the leg beat but also creates a reaction in the pulling arm which, as it begins the forward and downward sweep is often seen to move laterally and consequently forces of lift and drag will be generated.
The swimmer then may be making propulsive use of a deviating pull path that is produced not as a result of a random search for still water, but as a patterned action based on a specific mechanical or anatomical principle.
The middle section of the front crawl pull path is characterized by a marked inward and upward sweep of the hand and forearm, which takes place as a reaction to the rotational effect of the body around its long axis as the opposite arm and shoulder swing into the entry.
In back crawl the characteristic J-type pull, with the hand sweeping up towards the surface as it pulls, is caused simply by the action of bending the elbow. This occurs to allow a greater propulsive force application and as the elbow moves downwards the hand in reaction moves up. (pp. 84-85)
There is a degree of eloquence about this simple explanation for sideways components in swimming pulls. They occur because of the structure of the human anatomy. Rotational forces are developed by:
Those forces have to be counter-balanced by lateral actions of the kick and/or pull. When they occur in the pull, they are done as a reaction to keep the swimmer on a straight path, not to develop lift forces. Those forces are a consequence of the reaction. It is possible that if the human anatomy were structured differently, no lateral component of any pull would occur; the body simply would strive to generate a total drag force to achieve propulsion.
Cappaert's work and the accommodation-of-the-anatomy hypothesis of Wood, indicate that the primary force of propulsion in direct force strokes is drag. That interpretation is supported by the earlier work of Wood and Holt.
When an arm is in the water it is not always contributing to propulsion. Only when certain directions of action and pitch of the hand exist is propulsion attained. Thus, it is only appropriate to look at part of the pull to determine what is important for propulsion. The rest of the time the arm is in the water it is increasing frictional, form, and possibly wave resistance. It would seem to be prudent for a swimmer to minimize the time that an arm is creating extra resistance and to maximize its time in propulsion. Several figures already presented (see Figures 8 and 10) show when propulsion is initiated and when it ceases for several champions.
Valiant (1981) analyzed the progression of crawl stroke swimmers using an accelerometer. By matching filmed sequences with synchronized records of acceleration he was able to describe the parts of the arm stroke that contributed to forward progression. Figure 11 illustrates the phases of the crawl stroke in two swimmers that covered the duration of the acceleration records. Those patterns are very similar to the stages of propulsive force indicated in Figures 7, 8, and 10.
It is safe to assert that drag forces are predominant in the propulsive phase of the crawl, back, and butterfly strokes in swimming.
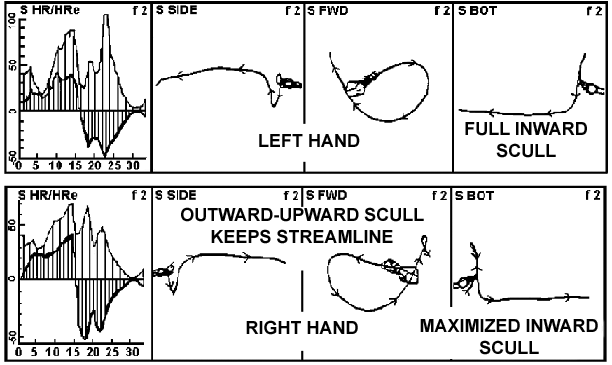
Breaststroke. There have been several references made that indicate drag force is more important than lift force in competitive strokes other than breaststroke. It is contended that the Newtonian analysis is still applicable to breaststroke. However, in breaststroke the lift component of the forces in the arm pull is increased. That is because of the very accentuated sideways movements in the outward and inward scull phases of the pull. Because of reasons cited previously (e.g., the inadequate leading and trailing edge shape of the hand and forearm) it is still not appropriate to use Bernoullian reasoning for the actions that are observed.
Breaststroke swimming does not follow the similarities in force generation of the other strokes. The arms' movement paths have a very dominant lateral component. However, the forces acting on the hand-arm combination are similar to those in the other strokes. What is different is that the direction of the drag force is very much to the side and contributes little to propulsive forces. Once the arms move directly sideways or have any forward component on the insweep, the drag force does not contribute to forward progression. The resultant force from the combination of both forces on both arms will generate propulsion. It stands to reason that if lift forces are small because of the properties of the hands and forearms, and drag forces contribute little to forward propulsion, the strength of the breaststroke pull will be quite small. Drag forces are not of great concern because each arm's force will mostly cancel out that of the other. Figure 12 illustrates the force curves for Mike Barrowman in the 1992 Olympic Games 200 m final. It is interesting to note that for both arms the total resistance of the hand and arm on recovery exceeds the amount of force created during the pull.
Practical Implications
It is time for most swimming science educators and practitioners to alter their thinking about pulling patterns of swimming strokes. The acceptance of Bernoullian lift as an "explanation" for the major propulsion forces has led to a tolerance for large lateral movements in pulling patterns. It has been argued that such movements do not maximize propulsive forces and are not demonstrated by today's best swimmers. Some lateral movements: (a) have to be retained to react to various forces that are not in the line of intended direction, and (b) are necessary because of the imperfections of the human anatomy for developing efficient force production. This orientation will require a different teaching and coaching strategy to the one that is popularly espoused.
This does not imply that lift forces are not important or should not occur. Drag forces should not be exclusively emphasized. The best propulsion will result from a stroke that has an optimal combination of both drag and lift-force components such that their combined contribution to the forward direction is maximized for the energy expended.
Propulsion
Although this paper and previous research have focused on the hand as the origin of forces, we have proposed that the forearm functions as a propulsive surface. Since the hand and forearm are jointed, it is appropriate to consider each segment independently for propulsive properties. One cannot assume that what happens on the hand also happens on the forearm. It is possible that the forearm could be very effective in its propulsion while the hand could be pitched differently and not as efficient. Consequently, it is important to consider both segments independently for effectiveness. That will require a radical change in the way measurements and forces on swimmers' arms are described. When that is accomplished, it is expected that the case for drag force dominance (in three of the four strokes) and Newtonian interpretations will be even stronger.
As an example of the above point, Figure 8 illustrates Kieren Perkins' forearm being pitched vertically while his hand is offset at a slight angle. The lift and drag force sizes and directions would be different for each arm part. On the other hand, Hrvoje Baric's arm (see Figure 10) is pitched at a very low angle decreasing the effectiveness of drag forces and increasing the relative contribution of lift forces. Since the alignment of the forearm and hand is almost straight, the contributions to propulsion of each arm segment may be different in size but are quite likely to be similar in direction of effect.
This discussion of propulsive forces has attempted to present a status report on the principles involved in propulsion in competitive swimming strokes. Drag forces are the major important components of propulsion. Lift forces exist but are of minor magnitude and usually operate in a direction that is not particularly helpful for propulsion. Objective measures of forces and the analyses of modern champion swimmers confirm this position. With regard to the theoretical basis of the forces, the originally proposed Bernoullian Principle is found to be inappropriate and insufficient for accounting for the propulsive forces. An application of Newton's Second and Third Laws provides a better basis for understanding what occurs. A change in the general thinking of the majority of biomechanists and coaches involved with swimming is in order.
Go to the next section, RESISTIVE FORCES, of this article.
Return to Table of Contents for Swimming Science Bulletin.
![]()