

LIFT IS NOT AN IMPORTANT FORCE IN SWIMMING PROPULSION
Brent S. Rushall, Ph.D.,R.Psy
Sports Science Associates and San Diego State University
April 2002
The development of lift forces has been a popular explanation of propulsion in swimming. Counsilman's original description (Counsilman, 1970), based solely on the Bernoulli Principle, was readily adopted although consistently challenged by a minority over the years until Sprigings and Koehler (1990) challenged it openly. A definitive criticism of swimming propulsion through lift was offered by Rushall et al (1994), which caused a number of notable swimming scientists to alter their explanations of propulsion in the sport. However, lift adherents still exist, much to the detriment of many serious swimmers.
Anderson and Eberhardt (2000) exposed serious weaknesses in the Bernoulli-Principle explanation for lift in flight. This paper contains a summary of their main points. Using their evidence-based explanations, it is clear that attributing significant propulsive force in swimming to the Bernoulli Principle, or even lift, is folly. In its place, an explanation based on physical laws is offered.
Lift is more credible if it is explained with Newton's Laws rather than the Bernoulli Principle. Essentially, lift in flight is due to the wing diverting air downward, most of which is pulled down from above the wing.
The Bernoulli Principle in Flight
The Bernoulli Principle applies to wing shapes in fluids, most commonly air and water. This simple principle is easy to understand, but that characteristic does not make it correct. It is based on a few factors involving a wing (an airfoil or hydrofoil).
The principle is dependent upon the shape of a wing. It does not account for flight being possible in an inverted aspect, the various requirements of power to meet certain environmental conditions (such as different altitudes, different plane loads, and in turns), ground effect, and the role of the angle-of-attack of the wing. It ignores the work performed by a wing.
The usual claim of the popular "Bernoullian" description of lift is that "when air separates at the leading edge, the part that goes over the top must converge at the trailing edge with the part that goes under the bottom" (Anderson & Eberhardt, 2001, p. 2). The origin of where the assumption that the separated air must meet at the trailing edge is unclear. In reality, it does not occur. The air passing under an airfoil is slowed while that over the top is accelerated. The assumption of equal transit times is not supported by empirical evidence.
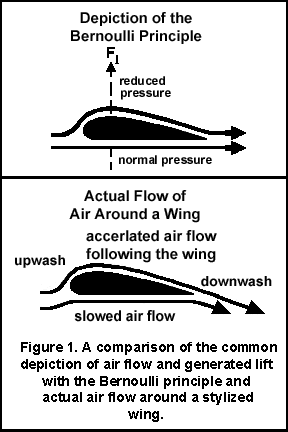
A typical picture of Bernoullian lift (see the upper portion of Figure 1) shows air leaving the wing in the same manner that it approached the wing. "There is no net action on the air so there can be no lift" in this model (p. 2).
Newton's Laws Explain Physical Forces that Lift
For a plane to be "lifted", a wing has to act on the air, and the air then has to react to that action (Newton's Third Law). The differential speeds of air flowing over and under a wing, and the adherence of the top airflow to the shape of the wing, causes air leaving the top surface to be directed down at an angle (see lower portion of Figure 1). To generate lift, a large amount of air must be diverted down.
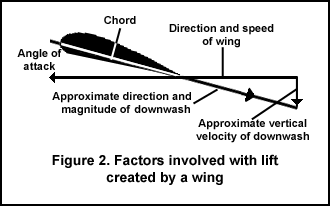
The change in momentum of the air directed downward affects the amount of lift that is developed. Thus, "the lift of a wing is proportional to the amount of air diverted down times the vertical velocity of that air" (p. 4). Vertical velocity is the vertical component of the "downwash" (the downward deflection of the air from over the wing top -- see Figure 1). The vertical velocity gives the wing lift.
There are several factors that affect the vertical component of the downwash (see Figure 2).
A wing develops lift by transferring momentum to the fluid.
"So how does a thin wing divert so much air? When the air is bent around the top of the wing, it pulls on the air above it [and from in front] accelerating that air downward. Otherwise, there would be voids in the air above the wing. Air is pulled from above. This pulling causes the pressure to become lower above the wing. It is the acceleration of the air above the wing in the downward direction that gives lift." (p. 5)
At the front edge of a wing an "upwash" occurs, which contributes to negative lift. More air has to be diverted downward to compensate for the upwash and still produce significant lift.
The shape and texture of the upper surface of a wing are critical. Structures, ice, etc, would cause the appropriate flow of fluid to be altered so that smooth flow would be diminished. The under surface is not as important and can have appendages, such as fuel tanks, struts, and armaments.
As air flows over a wing at an angle of attack, several events occur.
Flying an airplane then becomes a matter of controlling the volume of air diverted downward, and thus manipulating the size of the low pressure zone above the wing. This can be accomplished by changing the angle of attack, increasing the relative velocity of the oncoming fluid (more power), or by changing the shape of the wing. The pilot manipulates the zone of low pressure over the wing. Flight is not solely an artifact of the Bernoulli Principle.
The Coanda Effect
When a fluid contacts a surface, friction slows the fluid velocity causing it to curve and follow the surface shape until separation occurs. The better a fluid can follow the contour of a wing, the better will be the eventual lift. This following-of-shape effect is called the "Coanda effect".
The viscosity of a fluid determines how much slowing will occur on the object's surface. Even with air, the velocity of the fluid molecules at the surface, the "boundary layer", is zero. As layers extend further out from the surface, molecules gradually accelerate, shear forces causing the inner layers to slow markedly while very distant layers eventually are not affected at all.
"The magnitude of the forces on the air (and on the wing) is proportional to the "tightness" of the bend. The tighter the air bends, the greater the force on it. . . . most of the lift is on the forward part of the wing. In fact, half of the total lift on a wing is typically produced in the first quarter of the chord length" (p. 7)
Angle of Attack
The angle of attack of a wing (see Figure 2) is the primary determinant of lift, being more important than wing shape. The angle of attack is adjusted for fluid velocity and load, but when conditions are appropriate, the maximum critical angle is just less than 15 degrees. Above that angle, fluid separation occurs; the fluid ceasing to follow the shape of the upper surface of the wing causing lift to be lost and drag resistance to increase. A plane stalls when air on the top of a wing separates.
The Bernoulli Principle in Swimming
The above discussion explains some of the factors associated with the development of lift forces. For lift to be a viable productive force in swimming, it has to accommodate those factors.
". . ., in 1969, Counsilman committed himself to a radical change in the theoretical basis of propulsive forces in swimming. He proposed Bernoulli's Principle as the explanation of those forces. His followers were very quick to adopt this stance and conclude that "lift" forces were the major forces that produced propulsion in all competitive swimming strokes. For a brief time, "lift" was considered the only force for propulsion. However, as the limitations of sole lift explanations became apparent, "drag" forces (of Newtonian origin) crept back into the propulsion equation. Without any empirical evidence, but rather by intuitive analyses, "researchers" analyzed strokes of swimmers promoting lift forces as being the predominant propulsive force. For example, Schleihauf (in Counsilman, 1977, pp. 232-247) attributed the primary value of drag forces as being "The drag component of the hand could neutralize eccentric kicking forces and the lift component could approach its maximum value" (Schleihauf, 1977, p. 239). Such a position was echoed by Barthels (1982): ". . . proposed the ideal condition of maximizing the propulsive force and minimizing propulsive drag" (p. 386). Many persons, particularly those outside of the USA, appeared to become enamored with the Bernoulli Principle explanation of propulsive forces and persist with it today (e.g., Swimming Coaching Accreditation Scheme, Australia). Counsilman did modify his initial exclusivity of lift force being the only force in propulsion. Over time, he talked more of hand pitch ("angle of attack") as a significant determinant for creating force but never really focused on drag force [again] as a major determinant of propelling efficiency. He continued to emphasize a sideways orientation of stroke movements in the S-shaped or hourglass pull as facilitating lift and therefore, producing the forces to create speed in swimming" (Rushall et al, 1994).
Typical references to the appropriateness of the Bernoulli Principle to swimming have appeared in the literature. Counsilman (1971) stated:
"A wing provides aerodynamic lift through the camber (curvature) of its surfaces. Because the upper surface is more highly cambered than the lower surface, the air moving over the top surface is forced to move more quickly. This results in a lower pressure on the upper surface as compared with the lower surface and results in aerodynamic lift (Bernoulli's Principle)". (p. 61)
Maglischo (1982) accounted for lift as follows:
"The amount of lift force is proportional to the difference in pressure between the two wing surfaces which is, in turn, dependent upon the shape of the wing surfaces and the forward speed of the airplane." (p. 12)

Hinrich (1995) vigorously defended lift forces in swimming as a reaction to the Rushall et al. (1994) publication. These references are typical of the allegiance of most swimming "authorities" to the lift force derived from the Bernoulli Principle. Such references are misleading (Sprigings & Koehler, 1990, p. 237). Some individuals, Dr. Ernie Maglischo is one, have made admirable recantations of the "Bernoulli Belief", with a drag force interpretation being eloquently substituted as the more fruitful avenue for technique understanding and decisions.
In Figure 3, upward pressure on the front of the object, a discus, comes from the force of the air colliding with the undersurface (Newton's Third Law). That force is labeled R, the reaction force to the action of the air collision on the front. Many describe this as a "cushion" of air. The force R has vertical and horizontal components (V and H). Because the pocket of drag turbulence is asymmetrical, the drag force will not act in the direction of the fluid flow, but will be distorted off at an angle. When the horizontal force component is integrated with the drag force D, the object stops quite quickly. In aeronautical terms, the object "stalls" under these conditions. No lift force can occur in this condition because the Coanda Effect does not exist.
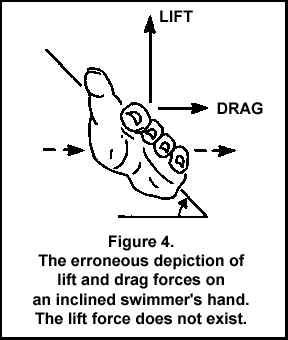
However, the "Lift theory" that unfortunately permeated swimming lore for several decades, promoted a fictitious set of circumstances (see Figure 4, adapted from Schleihauf, 1977a, p. 238). In this diagram an asymmetrical body, the hand, is presented at an angle of attack to horizontal flow (follow the arrows). A lift force is indicated as being greater than the drag force. Two errors are depicted. First, there is no lift force because there is no Coanda Effect. Second, with an object shaped like a hand, a lift force could never be greater than a drag force, even if a lift force ever existed.
When considering forces in complex situations, it is correct to talk of vertical and horizontal force components, or force components that are orthogonal to each other. However, it is incorrect to talk of "lift" without appropriate fluid flow over the upper surface of a "wing."
The Wing
Area of the wing surface.
Lift off a wing is proportional to the wing's area. The greater the area of a wing, the greater the amount of fluid diverted downward. As relative velocity of the fluid increases, so does the amount of fluid diverted. Since the load of the wing does not increase, the angle of attack must be reduced to produce constant lift.". . . lifting efficiency of a wing increases with increasing wing area. The larger the wing, the less induced power required to produce the same lift, although this is achieved with an increase in parasitic drag" (p. 11). This contradicts the common Bernoullian interpretation that lift does not require power.
Wing shape.
The downwash comes off a wing as a sheet and is related to the details of the load distribution on the wing. The volume of downwash decreases outward along the wing, producing what Anderson and Eberhardt call a "scoop effect"."Since the wing near the root is diverting so much air, the net effect is that the downwash sheet will begin to curl outward around itself, just as the air bends around the top of the wing because of the change in the velocity of the air. This is the wing vortex. The tightness of the curling on the wing vortex is proportional to the rate of change in lift along the wing. At the wing tip, the lift must rapidly become zero causing the tightest curl" (p. 13).
The wing tip vortex is often visible as white contrails. A winglet increases the length of a wing by blocking the traditional wing tip vortex. Since wing efficiency increases with area, a winglet gives greater efficiency. The downside of this ploy is that poorly designed winglets can actually be more detrimental than beneficial.
A desirable length and depth of a wing depends largely upon fluid velocity and load. At slow speeds, as with a sailplane, long narrow wings are appropriate. At very high speeds, long narrow wings would cause separation to occur. So a different shape of wing, usually much less in length and with increased depth associated with a sweeping to the rear of the frontal edge is more appropriate. Airplanes with a great speed range need to have the ability to alter their wing shapes to match the velocity and density of the air of the moment.
Load on the wing.
Induced power is proportional to the load squared. A wing stalls when the air separates from the upper wing surface, rather than following its contour. That occurs when the critical angle of attack for the relative fluid velocity is exceeded. "The angle of attack at which the plane stalls is constant and is not a function of wing loading. The angle of attack increases as the load and the stall speed increases as the square root of the load. . . . An increase in altitude will [require a] further increase in the angle of attack . . . an airplane can stall at any speed, since for any speed there is a load that will induce a stall." (p. 12).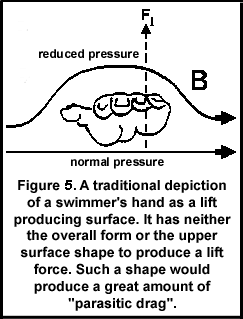
The Hand as the Swimmer's Wing
Traditionally, swimming texts have described the hand as the lifting surface (see Figure 5; adapted from Counsilman, 1977). The shape of the hand is not that of a lifting surface, its upper surface is incapable of producing a smooth or contour-conforming fluid flow. As well, the proposed oscillating lateral orientation of hand movements in crawl stroke swimming, the "S-shaped" pattern, would mean that during the outsweep, the small finger would be the leading edge, and on the insweep, the thumb would be the leading edge. Neither of those orientations produces an asymmetrical surface similar to a wing with a capability of producing significant lift forces. A swimmer's hand is not appropriately shaped, of any substantial area, or an efficient structure to produce lift forces of any notable magnitude. Its proposed beneficial functioning in medial-lateral and vertical movements (Payton & Mullineaux, 1996) is incorrect, although recently their model has been modified (Payton, Hay, & Mullineaux, 1997). Actually, swimmers adjust joint movements to reduce lateral and vertical movements (Hay, Liu, & Andrews, 1993).
The shape and surfaces of the hand are more conducive to developing drag forces than lift forces. A hand does not fit the characteristics of a lift force producing structure.
Accommodations
Various swimming theorists (e.g., Schleihauf, 1977a, 1977b) have proposed factors to account for swimmers' hands not fully displaying the Bernoulli prerequisite of a perfect wing at an angle of attack. Although all illustrative materials relate to the Bernoulli Principle, the role of angle of attack was not emphasized although it was recognized. Other observations were:
Despite these recognitions, adherence to the overly simplistic Bernoulli Principle focused coaching on developing lift in swimmers' strokes. The analogy of a swimmer's hand to an airplane wing was simply wrong. It did not have the shape or behavioral characteristics of a lift force generating wing. The analogy was false.
The Limitations of Focusing on the Hand
Lift-force advocates have focused on the hand as the propelling surface. Schleihauf (1979) reported using a model hand, with no wrist or forearm, to measure simulated lift forces. Despite finding that the hand was better suited to developing lift when water flowed from the wrist down the back of the hand to the fingers, lateral flow across the back of the hand was adamantly considered to be the source of swimming propulsion. However, in all swimming strokes, it has now been confirmed that the propulsive surface of a swimmer's arm includes the hand and forearm, and the upper arm at some stages of its abduction and adduction. A swimmer's "oar-blade" (propulsive surface) has increased dramatically in surface area over the past 20 years of swimming development in all competitive strokes. Rushall et al (1994) proposed that the forearm contributes more significantly to propulsion than does the hand.
Since the forearm and upper arms are virtually cylindrical in shape, their ability to develop lift is negligible. Their contribution to propulsion must be through drag forces, not lift.
Focusing on the hand and mystical (Bernoullian) lift has distracted coaches from attending to true propulsive capabilities in swimmers. Attention was placed on the path followed by the finger tips in a pull and presented as perfectly smooth movement loci in cartoon-like depictions of swimmers (see many illustrations in Counsilman, 1977). Tracking the finger tips is a false premise for considering important characteristics of a swimmer's movements. Producing "ideal" cartoons, many of which have no evidence-based origin, are mainly oversimplifications of irregular movement patterns. Tracing finger tips and producing cartoons have obscured the true nature of propulsive swimming movements for several decades.
It is more productive to focus on the orientation of the forearm and hand in all competitive strokes, even breaststroke, given the developments in pulling patterns that have occurred over the past decade.
The Minimization of Lateral Arm Actions
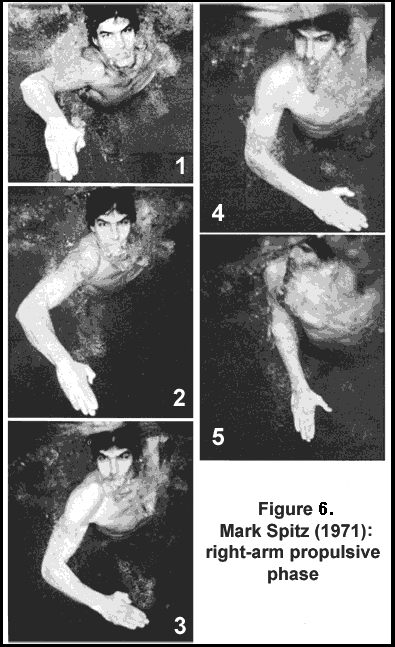
This writer advocates the center of the forearm-hand propulsive surface, about 2-3 inches above the wrist, is a better focus site than the hand for understanding movements. As the forearm-hand propelling surface rotates in the transverse plane, the axis of the rotation is very close to the center of the propulsive surface. That means the propulsive forces are almost directly backward with little lateral movement when viewed from a frontal orientation. That has always been a characteristic of most top swimmers since the early 1970s and in a few others before then. The focus on "lift theory" seems to have blinded many swimming scientists to not interpret data objectively. Figure 6 (adapted from Counsilman, 1977, pp. 150-151) illustrates Mark Spitz' right arm during the propulsive phase of the crawl stroke. The reader can determine if any of the following "anti-lift" characteristics are evident in the movement sequence.
Figure 6 shows predominantly backward movements, with the various joints involved accommodating restrictions demanded by a human anatomy that is not suited to travel through water. Very little lateral component in the movement is evidenced if the center of the forearm-hand propulsive surface is tracked. One could argue that what lateral movement occurs is caused by the outward and then inward rotation of the upper arm in the shoulder joint during abduction and adduction.
Hay, Liu, and Andrews (1993) commented on the "S-shaped" path of a crawl stroke pull being promoted as worthy of development and even exaggeration so that lift forces would be increased. They showed that when the arm was simulated to move directly backward with respect to a swimmer's reference frame [the shoulder joint], the path of the hand in the external reference frame was more curved than when actually swimming. This means that swimmers manipulate their movements to somewhat straighten the path of hand movements. Rather than swimmers abducting the arm to produce the "outsweep" and then adducting the arm to produce the "insweep", as commonly demonstrated by coaches, swimmers actually reduce the curvature in the arm movements outward and inward by concurrently rotating the body downward/inward and upward/outward.
These features demonstrate that top swimmers move to reduce lateral movements and present a hand forearm surface that maximizes drag force production. Movement dynamics that would promote minor lift forces are not performed.
Air and Water Density
As a plane increases altitude, the density of the air decreases, reducing the weight of the air that is diverted downward. Thus, any or all of three things must happen to produce constant lift when increasing altitude.
Water is approximately 1,000 times denser than air. To produce appreciable forces, movements in water can be much slower than in air. To create lift forces, there would still need to be some movement of the fluid across the back of the hand to produce a Coanda Effect, if that were possible. Water provides the best medium to develop drag forces rather than lift forces. Wood (1977) showed that during the crawl stroke propulsive phase, the hand slows down in relation to the water. Thus, during the productive phase of the stroke, the velocity of the fluid relative to the propulsive surface diminishes, further reducing any possibility of lift force creation.
The Requirement for Power
When a plane flies or a boat moves on hydrofoils, the fluid that passes is set into motion. Energy has passed from the vessel to the fluid. The energy comes from engines, or thermals or gravity as with a sailplane. This factor is not accommodated by the Bernoulli Principle.
". . . the energy given to the air by the wing is proportional to the amount of air diverted down times the vertical velocity squared of that diverted air. . . . the power needed to lift the airplane is proportional to the load (or weight) times the vertical velocity of the air. If the speed of the plane is doubled, the amount of air diverted down doubles. Thus, to maintain a constant lift, the angle of attack must be reduced to give a vertical velocity that is half the original. The power required for lift has been cut in half. This shows that the power required for lift becomes less as the airplane's speed increases" (p. 9)
However, reality requires more power to be applied to go faster. More power than that required for lift alone is needed. The power that produces lift is termed "induced" power. Its increase is proportional to (1/speed) of the plane. Power is also required to overcome drag resistance off struts, sensors, etc., which is called "parasitic drag". "Parasitic" power to overcome this drag increases as the speed cubed. At a cruising speed, parasitic power dominates. Increasing engine size does increase cruising speed, but only marginally. Cruise speeds will be affected more by aircraft design, particularly factors that reduce parasitic drag.
Summary of Lift Force Modifiers
These factors and relationships must be satisfied to produce significant lift forces. If they are to occur in sports, they must be fulfilled.
Anderson and Eberhardt (2001) offered three examples of the application of their physical explanation of lift forces that are not accommodated by the Bernoulli Principle. They used an airplane as the object.
The physical explanation of lift forces offered by Anderson and Eberhardt is more plausible to understand, more powerful, and able to account for phenomena associated with objects moving through fluids that cannot be explained by the Bernoulli Principle.
Reflections for Swimming
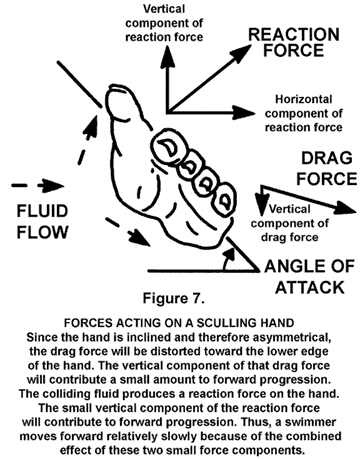
Most swimming coaches and scientists use the term "lift force" incorrectly. They calculate a lift force when none could exist because of the absence of the Coanda Effect. That is the problem with applying a formula based on only a partial understanding of the forces involved with different anatomical shapes. The erroneous lift force is more likely to be the sum of the direct force component of the asymmetrical drag force and the direct/vertical component of the reaction force between the hand and the fluid. Those forces are illustrated in Figure 3 on an inclined discus in a wind tunnel and again in Figure 7, which is a redrawing of Figure 4. This writer does not know of any published paper that has analyzed the forces on the hand correctly, all seeming to use lift incorrectly. Thus, when lift is used in referenced works here, it is done so with that reservation.
The following is but one of an increasing number of investigations that show lift forces [most probably erroneous lift forces] to be insignificant in swimming propulsion. There still exist several theorists who have steadfastly promoted a false theoretical model, mainly of crawl stroke swimming, that considers lift to be primary propulsive force.
Sanders (1997a, 1997b) measured hand lift and drag coefficients for crawl stroke in a testing tank. The coefficients were determined for the entire range of possible pitch and sweepback angles, defined in accordance with the convention established by Schleihauf (1979).
The greatest forces were obtained when the pitch angle was close to 90 degrees to the flow. At that orientation the force was due almost entirely to drag. Lift made its greatest contribution to resultant force at pitch angles near 45 degrees. However, even at 45 degrees, the contribution due to drag was as great as that of lift at most sweepback angles. When considered in three dimensions it was found that drag made a larger contribution to propulsive force than lift in all parts of the pull. During the most propulsive phase of the stroke the pitch was 50-60 degrees. That pitch took advantage of drag forces with a smaller contribution from lift. The fluid flow at this time was from the wrist to the fingers, a direction contrary to that depicted in most swimming texts (a foil generating lift forces from lateral movements that produce a flow across the back of the hand - see Figure 3). [At most positions no lift will occur, rather the vertical force component of the reaction force is confused with it and inappropriately labeled.]
Sanders' work implied that in crawl stroke, the hand does not function like an airfoil. The major proportion of propulsive force comes from drag force although an orthogonal force does make some minor contribution.
With the physical interpretation of lift (Anderson & Eberhardt, 2001), more real-world phenomena can be validly described and supported by scientific evidence. The inadequacies and restrictions imposed by the Bernoulli Principle, do not allow it to have any practical value for understanding the phenomena involved with flight [or more generally, the movement of objects in fluids].
Lift is not an important force in swimming propulsion because of the following.
It is hoped that swimming coaches and theorists will dispense with the consideration of lift forces and adhere to the characteristics of champion swimmers' movement patterns during the propulsive phase of their strokes. Coaches should employ evidence-based understandings of the production of both drag and lift forces. If lift forces are to be considered in swimming, they have to accommodate the physical features of force production discussed above, something which they cannot do.
The Bernoulli Principle cannot adequately account for lift forces in the real world. It is even further removed from applicability in swimming.
References
Return to Table of Contents for Swimming Science Bulletin.
